Dahlquist

• source: dahlquist.py

• example code: example_dahlquist.py

• scalar ODE

• discretization:

  • Backward Euler

  • Forward Euler

  • Trapezoidal rule

  • Implicit mid-point rule

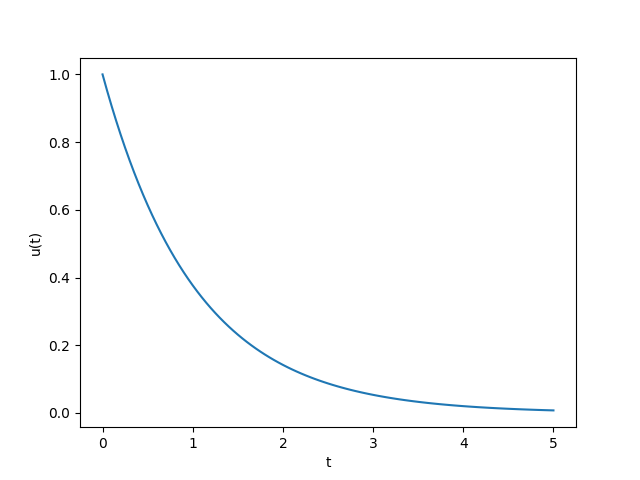
The simplest scalar ODE, made famous by Germund Dahlquist, is given by

\[u' = \lambda u \;\;\text{ in } (t_0, t_{end}]\;\; \text{ with }\; u(t_0) = 1,\]

and constant \(\lambda < 0\). The exact solution \(u(t) = e^{\lambda(t-t_0)}u(t_0)\) decays to zero as time increases.

For \(t_0 = 0, t_{end} = 5,\) and \(\lambda = -1\), for example, we obtain the following solution: