Arenstorf orbit

• source: arenstorf_orbit.py

• example code: example_arenstorf.py

• system of two scalar second-order ODEs with two unknown functions solved as system of four scalar first-order ODEs

• discretizations: RK45 from scipy.integrate

Arenstorf orbit is a special case of the three body problem from Astronomy, where two bodies of masses \(\mu\) and \(1-\mu\) (e.g., the moon and the earth) are orbiting in a plane, along with a third body of negligible mass relative to the other bodies (e.g., a satellite) in the same plane. The equations are

\[\begin{split}x'' &= x + 2y' - (1 - \mu)\frac{x + \mu}{D_1} - \mu\frac{x - (1-\mu)}{D_2},\\ y'' &= y - 2x' - (1-\mu)\frac{y}{D_1} - \mu\frac{y}{D_2},\end{split}\]

where \(D_1\) and \(D_2\) are functions of \(x\) and \(y\),

\[D_1 = ((x + \mu)^2 + y^2)^{3/2}, \;\;\; D_2 = ((x - (1-\mu))^2 + y^2)^{3/2}.\]

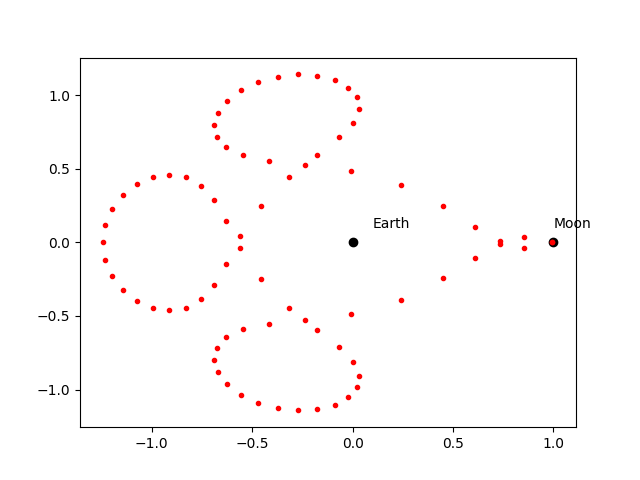
Here, the earth is at the origin and the moon is initially at (0,1). The mass of the moon is \(\mu = 0.012277471\) and the mass of the earth is \(1-\mu\).

If the initial conditions are chosen to be

\[x(0) = 0.994, \;\;\; x'(0) = 0, \;\;\; y(0) = 0, \;\;\; y'(0) = -2.00158510637908252240537862224,\]

then the solution is periodic with period \(T = 17.0652165601579625588917206249\). This example is taken from 1.

The Arenstorf orbit computed by example_arenstorf.py :

1

Gander M.J., Hairer E. (2008) Nonlinear Convergence Analysis for the Parareal Algorithm. In: Langer U., Discacciati M., Keyes D.E., Widlund O.B., Zulehner W. (eds) Domain Decomposition Methods in Science and Engineering XVII. Lecture Notes in Computational Science and Engineering, vol 60. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-75199-1_4