Brusselator

• source: brusselator.py

• example code: example_brusselator.py

• system of two scalar first-order ODEs with two unknown functions

• discretization: RK4

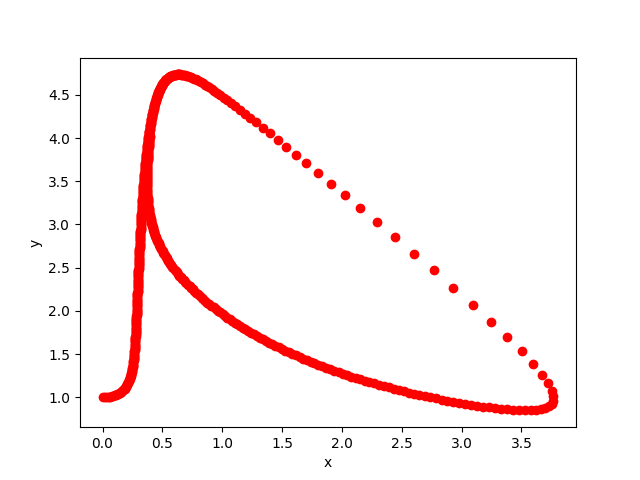
The Brusselator is a theoretical model for a chain of chemical reactions. It can be described by the following system of ODEs:

\[\begin{split}x' &= A + x^2y - (B + 1)x,\\ y' &= Bx - x^2y,\end{split}\]

with positive concentrations \(A\) and \(B\). If \(A\) and \(B\) are constant and \(B > A^2 + 1\), the system will form a limit cycle. This example is taken from 1.

In example_brusselator.py, \(A = 1\), \(B = 3\), and the initial conditions are chosen to be

\[x(0) = 0 \;\;\;\text{and} \;\;\; y(0) = 1,\]

which produces the output:

1

Gander M.J., Hairer E. (2008) Nonlinear Convergence Analysis for the Parareal Algorithm. In: Langer U., Discacciati M., Keyes D.E., Widlund O.B., Zulehner W. (eds) Domain Decomposition Methods in Science and Engineering XVII. Lecture Notes in Computational Science and Engineering, vol 60. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-75199-1_4