Advection

• source: advection_1d.py

• example code: example_advection.py

• scalar PDE with unknown function \(u(x,t)\) of two independent variables

• discretization:

  • first-order upwind finite differences in space,

  • backward Euler in time

The advection equation in 1D space is a partial differential equation that governs the motion of a scalar quantity, \(u(x,t)\), subject to a known nonzero (constant) flow speed, \(c\). The governing equation is given by

\[u_t + cu_x = 0 \;\;\text{ in } \;[a, b]\times(t_0, t_{end}]\;\; \text{ with }\; u(x, t_0) = u_0(x),\]

and subject to some boundary conditions in space.

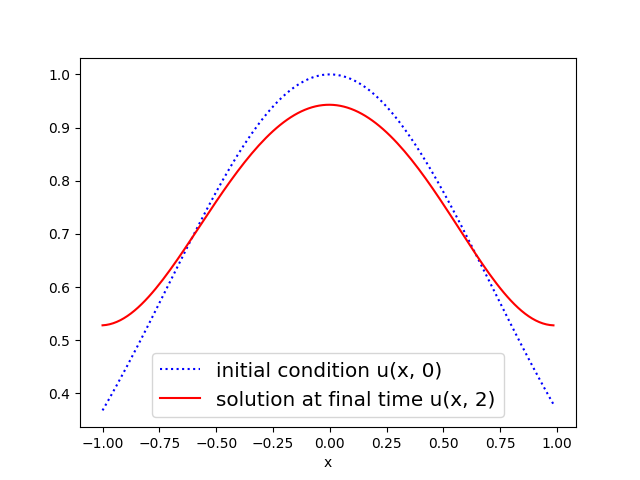
While parallel-in-time algorithms are known to work well for parabolic problems, most methods show instabilities or poor convergence for hyperbolic problems. The advection equation has proven to be a critical test problem and is therefore included in PyMGRIT. However, the discretization considered in PyMGRIT’s 1D advection application is highly diffusive and does not capture the exact solution.

In example_advection.py, advection subject to flow speed \(c = 1\), in the domain \([-1,1]\times[0,2]\) is considered with periodic boundary conditions in space and subject to the initial condition \(u(x,0) = e^{-x^2}\).